Polyominoes: Puzzles & Solutions
| Author: | David Goodger <goodger@python.org> |
|---|---|
| Date: | 2015-02-24 |
| Revision: | 600 |
| Web site: | http://puzzler.sourceforge.net/ |
| Copyright: | © 1998-2015 by David J. Goodger |
| License: | GPL 2 |

Contents
- Polyominoes of Order 1 Through 3
- Tetrominoes
- Polyominoes of Order 1 Through 4
- One-Sided Polyominoes of Order 1 Through 4
- One-Sided Polyominoes of Order 2 Through 4
- Polyominoes of Order 4 & 5 (Tetrominoes & Pentominoes)
- Polyominoes of Order 2 Through 5
- Polyominoes of Order 1 Through 5
- Polyominoes of Order 1 Through 6
Polyominoes of Order 1 Through 3
This puzzle uses the 1 monomino, 1 domino, and 2 trominoes, for a total of 9 squares.
Square: 6 solutions

A trivial result, but the number of solutions comes in handy in more complex puzzles like the poly-5 diamond.
Tetrominoes
The 5 tetrominoes are well known from their use in the video game "Tetris". Tetris does not allow the pieces to be flipped (mirror-reflected); its pieces comprise the 7 "one-sided" tetrominoes.
Due to a parity imbalance, the 5 free tetrominoes cannot fit into a simple rectangle without introducing holes or other irregularities.
However, if we consider a 5x4 rectangle and join the short sides together to form a cylindrical tube, we can find solutions:
5x4 tube: 7 solutions

In this solution, the 4x1 "I4" piece spans the join between right and left edges. It appears to be chopped in two above, but if you join the left & right edges, it forms one continuous piece. Here it is, unwrapped:

See this article by Alexandre Owen Muñiz and a video by Edo Timmermans.
Polyominoes of Order 1 Through 4
These puzzles use the 1 monomino, 1 domino, 2 trominoes, and 5 tetrominoes, for a total of 29 squares.
Square-plus (design from Kadon / Kate Jones): 563 solutions

7x3-plus (design by Dan Klarskov): 17 solutions

Skewered square (design by Dan Klarskov): 1,320 solutions

Skewered 9x3 rectangle (design by Dan Klarskov): 5,249 solutions

Skewered 7x3 rectangle: 747 solutions

Astroid (design from Kadon / Kate Jones): 18 solutions

7x5 with cross-shaped hole (design by Dan Klarskov): 19 solutions

7x4 plus one (design by Dan Klarskov): 1,522 solutions

This is just a 7x4 rectangle using the polyominoes of order 2 through 4, plus the monomino separately. I thought it was cute.
One-Sided Polyominoes of Order 1 Through 4
These puzzles use the 1 monomino, 1 domino, 2 trominoes, and 7 tetrominoes, for a total of 37 squares.
Octagon: solutions incomplete

One-Sided Polyominoes of Order 2 Through 4
These puzzles use the 1 domino, 2 trominoes, and 7 tetrominoes, for a total of 36 squares.
Square: 7,252 solutions

Octagon: 1,023 solutions

Polyominoes of Order 4 & 5 (Tetrominoes & Pentominoes)
These puzzles use the 5 tetrominoes and 12 pentominoes, for a total of 80 squares.
Rectangles
8x10: solutions incomplete

5x16: solutions incomplete

4x20: solutions incomplete

9x9 Square (with a hole in the middle): solutions incomplete

Miscellaneous
Diamond: 7,302 solutions

Aztec Diamond: 11,162 solutions

Polyominoes of Order 2 Through 5
These puzzles use the 1 domino, 2 trominoes, 5 tetrominoes, and 12 pentominoes, for a total of 88 squares.
Polyominoes of Order 1 Through 5
These puzzles use the 1 monomino, 1 domino, 2 trominoes, 5 tetrominoes, and 12 pentominoes, for a total of 89 squares.
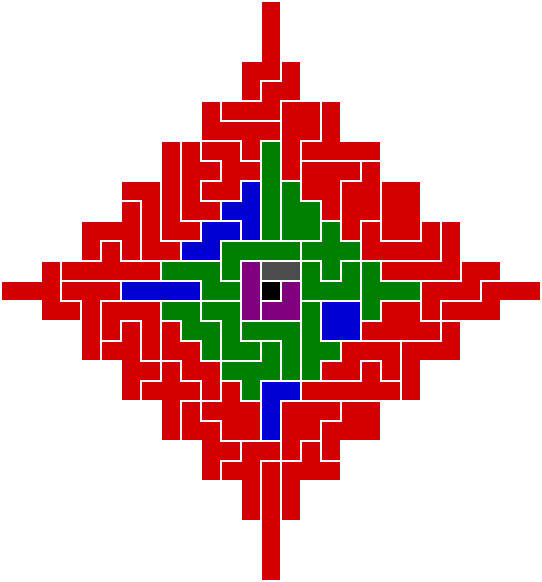
Diamond (a.k.a. Kadon's "Poly-5"): solutions incomplete

The configuration below has the monomono, domino, & trominoes restricted to a central 3×3 square, resulting in 4,579 unique solutions for the outer ring of pentominoes & tetrominoes alone. Combined with 6 unique independent solutions for the inner square, and 8 relative orientations (the inner square can rotate to 4 different positions, and 4 more flipped), the grand total is 219,792 unique solutions (4,579 × 6 × 8).

Also see the poly-6 star below.
Crosses:

solutions incomplete (design by Kadon)

Polyominoes of Order 1 Through 6
These puzzles use the 1 monomino, 1 domino, 2 trominoes, 5 tetrominoes, 12 pentominoes, and 35 hexominoes, for a total of 299 squares.
23x13 rectangle: solutions incomplete

Star (design by Jack Wetterer and Chris Patterson, with symmetry refinements by Darian Jenkins, extending Kadon's "Poly-5" a.k.a. poly-5 diamond above): solutions incomplete

As with the poly-5 diamond above, the various orders of polyominoes occupy different areas. The coloured version below shows the monomino (black), domino (gray), and trominoes (purple) fixed in a central 3×3 square, with the tetrominoes (blue) and pentominoes (green) occupying a middle ring around the square. The hexominoes (red) occupy the outer ring of the configuration.