An Introduction to Polycubes
| Author: | David Goodger <goodger@python.org> |
|---|---|
| Date: | 2018-09-05 |
| Revision: | 655 |
| Web site: | http://puzzler.sourceforge.net/ |
| Copyright: | ©1998-2018 by David J. Goodger |
| License: | GPL 2 |

Contents
Polycubes are polyforms constructed from unit cubes joined face-to-face in regular three-dimensional Cartesian space. The polycubes that are flat (only one cube thick) are known as "planar polycubes" or "solid polyominoes".
Here is a puzzle containing all the polycubes of order 1 through 5:

See Polycubes: Puzzles & Solutions, Pentacubes: Puzzles & Solutions, and Solid Pentominoes: Puzzles & Solutions for many more puzzles.
Polyforms
The number and names of the various orders of polycubes are as follows:
| Order | Polyform
Name
|
Polycubes | Planar
Polycubes
|
|---|---|---|---|
| 1 | monocube | 1 | 1 |
| 2 | dicube | 1 | 1 |
| 3 | tricubes | 2 | 2 |
| 4 | tetracubes | 8 | 5 |
| 5 | pentacubes | 29 | 12 |
| 6 | hexacubes | 166 | 35 |
"*" above means that forms with enclosed holes exist.
The numbers of polycubes can also be found in the following sequences from The On-Line Encyclopedia of Integer Sequences: A000162 (3-D) and A000105 (planar polycubes / solid polyominoes).
Examples of the polycubes from order 1 (monocube) to order 6 (hexacubes) are given in the tables below.
The polycubes are named with letters (like the monocube "M") or a letter-number scheme (like the "I3" tricube, and the "F5" and "V15" pentacubes). The names used by Polyform Puzzler are based on the traditional names for pentominoes, Kadon's names for their Superquints, hexacubes, and Poly-4 Supplement sets, as well as Thorleif Bundgård's names for Soma cubes.
The initial letter of each name is the letter of the alphabet that the polycube most closely resembles, or an initial. In some cases, that resemblance is weak, and the letters are arbitrary. The final digit of the number represents the polyform order (how many unit cubes are in the polycube). There are more pentacubes than letters in the alphabet, so the names of many of the non-planar pieces have an extra middle digit to differentiate the variations. All 166 of the hexacubes have 3-character names.
In the tables below, "Aspects" refers to the number of unique orientations that a polyform may take (different rotations, flipped or not). This varies with the symmetry of the polyform.
The "Notes" column records which pieces are planar and non-planar, as well as chiral pairs (matching left-hand and right-hand mirror images). The 3-D polycubes cannot be "flipped" into their mirror images (that would require access to a fourth physical dimension).
Alternate names and name origins are noted in the "Name" column.
Monocube
There is only one monocube (order-1 polycube):
| Name | Image | Aspects | Notes |
|---|---|---|---|
M
(from "Monocube")
|

|
1 | planar |
Dicube
There is only one dicube (order-2 polycube), also planar (a solid monomino):
| Name | Image | Aspects | Notes |
|---|---|---|---|
D
(from "Dicube")
|

|
3 | planar |
Tricubes
There are 2 tricubes (order-3 polycubes), also planar (a solid domino):
| Name | Image | Aspects | Notes |
|---|---|---|---|
| I3 | 
|
3 | planar |
V3
(Soma "V")
|

|
12 | planar |
Tetracubes
There are 8 tetracubes (order-4 polycubes), 5 of which are planar (solid tetrominoes):
| Name | Image | Aspects | Notes |
|---|---|---|---|
A4
(Soma "a"; Kadon "V3")
|

|
12 | non-planar; chiral pair with "B4" |
B4
(Soma "b"; Kadon "V1")
|

|
12 | non-planar; chiral pair with "A4" |
| I4 | 
|
3 | planar |
L4
(Soma "L")
|

|
24 | planar |
| O4 | 
|
3 | planar |
P4
(Soma "p"; Kadon "V2")
|

|
8 | non-planar |
S4
(Soma "Z")
|

|
12 | planar |
T4
(Soma "T")
|

|
12 | planar |
Soma Cubes
The Soma Cubes, invented by Piet Hein in 1933, consist of 7 pieces: all the non-convex polycubes of order 3 (1) and 4 (6).
| Name | Image | Aspects | Notes |
|---|---|---|---|
V
(polycube "V3")
|

|
12 | planar; order 3 |
L
(polycube "L4")
|

|
24 | planar; order 4 |
T
(polycube "T4")
|

|
12 | planar; order 4 |
Z
(polycube "S4"; Kadon "S")
|

|
12 | planar; order 4 |
a
(polycube "A4"; Kadon "V3")
|

|
12 | non-planar; order 4; chiral pair with "b" |
b
(polycube "B4"; Kadon "V1")
|

|
12 | non-planar; order 4; chiral pair with "a" |
p
(polycube "P4"; Kadon "V2")
|

|
8 | non-planar; order 4 |
Pentacubes
There are 29 pentacubes (order-5 polycubes), 12 of which are planar (solid pentominoes):
| Name | Image | Aspects | Notes |
|---|---|---|---|
| A5 | 
|
24 | non-planar |
| F5 | 
|
24 | planar |
| I5 | 
|
3 | planar |
| J15 | 
|
12 | non-planar; chiral pair with "L15" |
| J25 | 
|
24 | non-planar; chiral pair with "L25" |
| J45 | 
|
24 | non-planar; chiral pair with "L45" |
| L5 | 
|
24 | planar |
| L15 | 
|
12 | non-planar; chiral pair with "J15" |
| L25 | 
|
24 | non-planar; chiral pair with "J25" |
| L35 | 
|
24 | non-planar; Kadon's Super Deluxe Quintillions set includes a second copy called "J35" (also adopted by Polyform Puzzler's Pentacubes Plus) |
| L45 | 
|
24 | non-planar; chiral pair with "J45" |
| N5 | 
|
24 | planar |
| N15 | 
|
24 | non-planar; chiral pair with "S15" |
| N25 | 
|
24 | non-planar; chiral pair with "S25" |
| P5 | 
|
24 | planar |
| Q5 | 
|
24 | non-planar |
| S15 | 
|
24 | non-planar; chiral pair with "N15" |
| S25 | 
|
24 | non-planar; chiral pair with "N25" |
| T5 | 
|
12 | planar |
| T15 | 
|
12 | non-planar |
| T25 | 
|
24 | non-planar |
| U5 | 
|
12 | planar |
| V5 | 
|
12 | planar |
| V15 | 
|
12 | non-planar; chiral pair with "V25" |
| V25 | 
|
12 | non-planar; chiral pair with "V15" |
| W5 | 
|
12 | planar |
| X5 | 
|
3 | planar |
| Y5 | 
|
24 | planar |
| Z5 | 
|
12 | planar |
Hexacubes
There are 166 hexacubes (order-6 polycubes), 35 of which are planar (solid hexominoes):
| Name | Image | Aspects | Notes |
|---|---|---|---|
A06
(Kadon's "A")
|

|
12 | planar |
Aa6
("Fat A")
|

|
12 | non-planar |
Ba6
("B")
|

|
4 | non-planar |
| C06 | 
|
12 | planar |
| D06 | 
|
12 | planar |
| E06 | 
|
12 | planar |
F06
("hi F")
|

|
24 | planar |
F16
("low F")
|

|
24 | planar |
F26
("hi 4")
|

|
24 | planar |
F36
("low 4")
|

|
24 | planar |
Fa6
("F1")
|

|
24 | non-planar |
Fb6
("F2")
|

|
24 | non-planar |
Fc6
("F3")
|

|
24 | non-planar |
Fd6
("F4")
|

|
24 | non-planar |
Fe6
("F5")
|

|
24 | non-planar |
Ff6
("Fb1")
|

|
24 | non-planar |
Fg6
("Fb2")
|

|
24 | non-planar |
Fh6
("Fb3")
|

|
24 | non-planar |
Fi6
("Fb4")
|

|
24 | non-planar |
Fj6
("Fb5")
|

|
24 | non-planar |
| G06 | 
|
24 | planar |
| H06 | 
|
24 | planar |
| I06 | 
|
3 | planar |
| J06 | 
|
24 | planar |
Ja6
("J1l")
|

|
24 | non-planar |
Jb6
("J1r")
|

|
24 | non-planar |
Jc6
("J2l")
|

|
24 | non-planar |
Jd6
("J2r")
|

|
24 | non-planar |
Je6
("J3r")
|

|
24 | non-planar |
Jf6
("J4l")
|

|
24 | non-planar |
Jg6
("J4u")
|

|
24 | non-planar |
Jh6
("J4d")
|

|
24 | non-planar |
Ji6
("J4v")
|

|
12 | non-planar |
| K06 | 
|
12 | planar |
| L06 | 
|
24 | planar |
La6
("L1")
|

|
12 | non-planar |
Lb6
("L4")
|

|
24 | non-planar |
Lc6
("L5")
|

|
24 | non-planar |
Ld6
("Lb1")
|

|
12 | non-planar |
Le6
("Lb5")
|

|
24 | non-planar |
Lf6
("L1l")
|

|
24 | non-planar |
Lg6
("L1r")
|

|
24 | non-planar |
Lh6
("L2l")
|

|
24 | non-planar |
Li6
("L2r")
|

|
24 | non-planar |
Lj6
("L3l")
|

|
24 | non-planar |
Lk6
("L4r")
|

|
24 | non-planar |
Ll6
("L4u")
|

|
24 | non-planar |
Lm6
("L4d")
|

|
24 | non-planar |
Ln6
("L4v")
|

|
12 | non-planar |
| M06 | 
|
24 | planar |
N06
("short N")
|

|
12 | planar |
N16
("long N")
|

|
24 | planar |
Na6
("N1")
|

|
24 | non-planar |
Nb6
("N2")
|

|
24 | non-planar |
Nc6
("N3")
|

|
24 | non-planar |
Nd6
("N4")
|

|
24 | non-planar |
Ne6
("N5")
|

|
24 | non-planar |
Nf6
("Nb1")
|

|
24 | non-planar |
Ng6
("Nb2")
|

|
24 | non-planar |
Nh6
("Nb3")
|

|
24 | non-planar |
Ni6
("Nb4")
|

|
24 | non-planar |
Nj6
("Nb5")
|

|
24 | non-planar |
Nk6
("N13")
|

|
24 | non-planar |
Nl6
("N14")
|

|
12 | non-planar |
Nm6
("N1l")
|

|
24 | non-planar |
Nn6
("N1r")
|

|
24 | non-planar |
No6
("N1u")
|

|
12 | non-planar |
Np6
("N1b3")
|

|
24 | non-planar |
Nq6
("N1b4")
|

|
24 | non-planar |
Nr6
("N23")
|

|
12 | non-planar |
Ns6
("N2r")
|

|
24 | non-planar |
Nt6
("N2b3")
|

|
12 | non-planar |
Nu6
("N2b4")
|

|
24 | non-planar |
| O06 | 
|
6 | planar |
| P06 | 
|
24 | planar |
Pa6
("P1")
|

|
24 | non-planar |
Pb6
("P2")
|

|
24 | non-planar |
Pc6
("P3")
|

|
24 | non-planar |
Pd6
("P4")
|

|
24 | non-planar |
Pe6
("P5")
|

|
24 | non-planar |
Pf6
("Pb1")
|

|
24 | non-planar |
Pg6
("Pb2")
|

|
24 | non-planar |
Ph6
("Pb3")
|

|
24 | non-planar |
Pi6
("Pb4")
|

|
24 | non-planar |
Pj6
("Pb5")
|

|
24 | non-planar |
| Q06 | 
|
24 | planar |
Qa6
("Q14")
|

|
12 | non-planar |
Qb6
("Q4r")
|

|
24 | non-planar |
Qc6
("Q4d")
|

|
24 | non-planar |
Qd6
("Q4v")
|

|
24 | non-planar |
Qe6
("Q4b1")
|

|
12 | non-planar |
| R06 | 
|
24 | planar |
S06
("long S")
|

|
12 | planar |
Sa6
("S13")
|

|
24 | non-planar |
Sb6
("S14")
|

|
12 | non-planar |
Sc6
("S1l")
|

|
24 | non-planar |
Sd6
("S1r")
|

|
24 | non-planar |
Se6
("S1u")
|

|
12 | non-planar |
Sf6
("S23")
|

|
12 | non-planar |
Sg6
("S2l")
|

|
24 | non-planar |
Sh6
("S2d")
|

|
24 | non-planar |
T06
("long T")
|

|
12 | planar |
T16
("short T")
|

|
24 | planar |
Ta6
("T1")
|

|
24 | non-planar |
Tb6
("T2")
|

|
24 | non-planar |
Tc6
("T3")
|

|
24 | non-planar |
Td6
("T4")
|

|
24 | non-planar |
Te6
("T5")
|

|
24 | non-planar |
Tf6
("T1u")
|

|
24 | non-planar |
Tg6
("T1d")
|

|
24 | non-planar |
Th6
("T24")
|

|
12 | non-planar |
Ti6
("T2u")
|

|
24 | non-planar |
Tj6
("T3u")
|

|
24 | non-planar |
Tk6
("T3d")
|

|
24 | non-planar |
Tl6
("T4l")
|

|
24 | non-planar |
Tm6
("T4r")
|

|
24 | non-planar |
Tn6
("T4d")
|

|
24 | non-planar |
To6
("T4v")
|

|
24 | non-planar |
Tp6
("T4b4")
|

|
6 | non-planar |
| U06 | 
|
24 | planar |
Ua6
("U1")
|

|
24 | non-planar |
Ub6
("U2")
|

|
24 | non-planar |
Uc6
("U3")
|

|
24 | non-planar |
Ud6
("U4")
|

|
24 | non-planar |
Ue6
("U5")
|

|
24 | non-planar |
| V06 | 
|
24 | planar |
Va6
("V1")
|

|
24 | non-planar |
Vb6
("V2")
|

|
24 | non-planar |
Vc6
("V3")
|

|
24 | non-planar |
Vd6
("V4")
|

|
24 | non-planar |
Ve6
("V5")
|

|
24 | non-planar |
Vf6
("V1l")
|

|
12 | non-planar |
Vg6
("V1d")
|

|
24 | non-planar |
Vh6
("V3r")
|

|
12 | non-planar |
Vi6
("V3d")
|

|
24 | non-planar |
W06
("Wa")
|

|
24 | planar |
W16
("Wb")
|

|
12 | planar |
W26
("Wc")
|

|
24 | planar |
Wa6
("W1")
|

|
24 | non-planar |
Wb6
("W2")
|

|
24 | non-planar |
Wc6
("W3")
|

|
24 | non-planar |
Wd6
("W4")
|

|
24 | non-planar |
We6
("W5")
|

|
24 | non-planar |
| X06 | 
|
12 | planar |
X16
("italic X")
|

|
12 | planar |
Xa6
("X1")
|
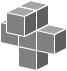
|
24 | non-planar |
Xb6
("X3")
|

|
6 | non-planar |
Y06
("hi Y")
|

|
24 | planar |
Y16
("low Y")
|

|
12 | planar |
Ya6
("Y1")
|

|
24 | non-planar |
Yb6
("Y2")
|

|
24 | non-planar |
Yc6
("Y3")
|

|
24 | non-planar |
Yd6
("Y4")
|

|
12 | non-planar |
Ye6
("Y5")
|

|
24 | non-planar |
Yf6
("Yb1")
|

|
24 | non-planar |
Yg6
("Yb2")
|

|
24 | non-planar |
Yh6
("Yb4")
|

|
12 | non-planar |
Yi6
("Yb5")
|

|
24 | non-planar |
Z06
("long Z")
|

|
12 | planar |
Z16
("short Z")
|

|
24 | planar |
Za6
("Z1")
|

|
24 | non-planar |
Zb6
("Z2")
|

|
24 | non-planar |
Zc6
("Z3")
|

|
12 | non-planar |
Zd6
("Zb1")
|

|
24 | non-planar |
Ze6
("Zb2")
|

|
24 | non-planar |
Zf6
("Zb3")
|

|
12 | non-planar |
Coordinate System
Polycubes (including solid pentominoes and Soma cubes) use a 3-dimensional (x,y,z) Cartesian coordinate system.
Each unit cube has 6 immediate neighbors. The neighbors of the cube at coordinates (x, y, z) are:
{(x+1, y, z), (x-1, y, z), (x, y+1, z), (x, y-1, z), (x, y, z+1), (x, y, z-1)}