An Introduction to Polysticks
| Author: | David Goodger <goodger@python.org> |
|---|---|
| Date: | 2015-02-24 |
| Revision: | 600 |
| Web site: | http://puzzler.sourceforge.net/ |
| Copyright: | © 1998-2015 by David J. Goodger |
| License: | GPL 2 |

Contents
Polysticks are polyforms constructed from unit line segments (edges) joined end-to-end on a regular square grid. Polysticks were named by and seem to have been first formally expolored by Brian R. Barwell [1].
Here is a puzzle containing all the polysticks of order 1 through 4:

See Polysticks: Puzzles & Solutions for many more puzzles.
The polysticks can be thought of as the projective duals of polyominoes. Most of the polysticks of order N can be derived from the polyominoes of order N+1 (i.e., joining the centers of the squares of a pentomino results in a tetrastick). The exceptions are the polysticks with loops (e.g. the "O" tetrastick), which are duals of the same order or lower-order polyominoes. Also, it is not a one-to-one mapping. For example, the P pentomino can be mapped to four different tetrasticks, the F, H, J, and P (depending on which loop segment of the full "P" pentastick is left out).
During a visit to India in 2010, it was pointed out to me that polystick puzzles look a lot like some of the "kolam" sand/chalk drawings that can be seen on sidewalks and patios outside of homes. These drawings are thought to bestow prosperity to homes.
| [1] | Brian R. Barwell, "Polysticks," Journal of Recreational Mathematics volume 22 issue 3 (1990), p.165-175 |
Polyforms
The number and names of the various orders of polysticks are as follows:
| Order | Polyform
Name
|
Free
Polysticks
|
One-Sided
Polysticks
|
|---|---|---|---|
| 1 | monostick | 1 | 1 |
| 2 | distick | 2 | 2 |
| 3 | tristick | 5 | 7 |
| 4 | tetrastick | 16 | 25 |
| 5 | pentastick | 55 | 99 |
| 6* | hexastick | 222 | 416 |
| 7* | heptastick | 950 | 1854 |
"*" above means that forms with enclosed holes exist.
The numbers of polysticks can also be found in the following sequences from The On-Line Encyclopedia of Integer Sequences: A019988 (free) and A151537 (one-sided).
Examples of the polysticks from order 1 (monostick) to order 4 (tetrasticks) are given in the tables below.
The polysticks (other than the tetrasticks) are named with a letter-number scheme, like "I1" and "L3". The initial letter is the letter of the alphabet that the polystick most closely resembles. In some cases, that resemblance is weak, and the letters are arbitrary. The number represents the polyform order (how many line segments are in the polystick). The tetrasticks have established letter-only names.
In the tables below, "Aspects" refers to the number of unique orientations that a polyform may take (different rotations, flipped or not). This varies with the symmetry of the polyform.
The "One-Sided" column identifies polyforms that are asymmetrical in reflection. Treating the flipped and unflipped versions of asymmetrical polysticks as distinct polyforms (and disallowing further reflection or "flipping"), results in "one-sided" polysticks and puzzles.
The "Welded" column identifies polyforms that contain junction points or branches (they cannot be formed by simple bending).
Tristicks
There are 5 free tristicks (order-3 polysticks) and 7 one-sided tristicks:
| Name | Image | Aspects | One-Sided | Welded |
|---|---|---|---|---|
| I3 | 
|
2 | ||
| L3 | 
|
8 | yes | |
| T3 | 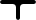
|
8 | yes | |
| U3 | 
|
4 | ||
| Z3 | 
|
4 | yes |
Tetrasticks
There are 16 free tetrasticks (order-4 polysticks) and 25 one-sided tetrasticks:
| Name | Image | Aspects | One-Sided | Welded |
|---|---|---|---|---|
| F | 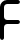
|
8 | yes | yes |
| H | 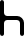
|
8 | yes | yes |
| I | 
|
2 | ||
| J | 
|
8 | yes | |
| L | 
|
8 | yes | |
| N | 
|
8 | yes | |
| O | 
|
1 | ? | |
| P | 
|
8 | yes | |
| R | 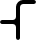
|
8 | yes | yes |
| T | 
|
4 | yes | |
| U | 
|
4 | ||
| V | 
|
4 | ||
| W | 
|
4 | ||
| X | 
|
1 | yes | |
| Y | 
|
8 | yes | yes |
| Z | 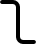
|
4 | yes |
Seven-Segment Digits
These pieces correspond to the seven-segment display decimal digits 0 through 9, as seen on digital watches, for a total of 49 line segments. Based on the "Digigrams" puzzle (AKA "Count On Me" or "Count Me In") by Martin H. Watson. The 0/zero digit must have a gap in one side to allow the central segment to be occupied (by a 1 or a 7 only). The 2 and 5 digits are identical (through reflection), and the 6 and 9 are identical (through rotation). The pieces comprise one distick (digit 1), one tristick (digit 7), one tetrastick (digit 4), three pentasticks (digits 2, 3, & 5), three hexasticks (digits 0, 6, & 9), and one heptastick (digit 8).
| Name | Image | Aspects | One-Sided | Welded |
|---|---|---|---|---|
| d0 | 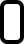
|
2 | ||
| d1 | 
|
2 | ||
| d2 | 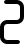
|
4 | yes | |
| d3 | 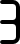
|
4 | yes | |
| d4 | 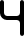
|
8 | yes | yes |
| d5 | 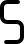
|
4 | yes | |
| d6 | 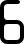
|
8 | yes | yes |
| d7 | 
|
8 | yes | |
| d8 | 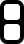
|
2 | yes | |
| d9 | 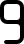
|
8 | yes | yes |
Coordinate System
Polystick puzzles use a pseudo-3D coordinate system. The (X,Y) 2-dimensional coordinate identifies the lower-left corner of the (X,Y,0) square in a polyomino grid. The Z dimension is used for the direction of the line segment:
Intersections
As there is the possibility for polysticks to cross each other at any (X,Y) intersection, the solution algorithm needs to prevent such crossings. The intersections are simple, either used (by a straight-through piece) or available.
In the puzzle matrix, we represent contstraints on intersections via an additional column per intersection [*], in the form i(X,Y,Z) (or "X,Yi").
| [*] | Intersections at the edge of a puzzle shape may be ignored. This represents a possible future optimization. |
These intersection constraints are secondary columns, meaning that at most one polyform may use or fill a column. Unlike primary columns, secondary columns may remain unused/unfilled.
If an intersection constraint is already used (or otherwise unavailable), no other polyform with the same contstraint may be placed in the puzzle solution. This prevents two polysticks from crossing each other.


