An Introduction to Polyhexes
| Author: | David Goodger <goodger@python.org> |
|---|---|
| Date: | 2015-02-24 |
| Revision: | 600 |
| Web site: | http://puzzler.sourceforge.net/ |
| Copyright: | © 1998-2015 by David J. Goodger |
| License: | GPL 2 |

Polyhexes are polyforms constructed from unit hexagons joined edge-to-edge on a regular hexagonal grid (a honeycomb grid).
Here is a puzzle containing all the polyhexes of order 1 through 5:

See Polyhexes: Puzzles & Solutions and Pentahexes: Puzzles & Solutions for many more puzzles.
Polyforms
The number and names of the various orders of polyhexes are as follows:
| Order | Polyform
Name
|
Free
Polyhexes
|
One-Sided
Polyhexes
|
|---|---|---|---|
| 1 | monohex | 1 | 1 |
| 2 | dihex | 1 | 1 |
| 3 | trihexes | 3 | 3 |
| 4 | tetrahexes | 7 | 10 |
| 5 | pentahexes | 22 | 33 |
| 6* | hexahexes | 82 | 147 |
"*" above means that forms with enclosed holes exist.
The numbers of polyhexes can also be found in the following sequences from The On-Line Encyclopedia of Integer Sequences: A000228 (free) and A006535 (one-sided).
Examples of the polyhexes from order 1 (monohex) to order 6 (hexahexes) are given in the tables below.
The polyhexes are named with a letter-number scheme, like "H1", "A3", and "I06". The initial letter is the letter of the alphabet that the polyhex most closely resembles. In some cases, that resemblance is weak, and the letters are arbitrary. The final digit of the number represents the polyform order (how many unit hexagons are in the polyhex). There are more hexahexes than letters in the alphabet, so their names have an extra middle digit (numbered from 0) to differentiate the variations.
In the tables below, "Aspects" refers to the number of unique orientations that a polyform may take (different rotations, flipped or not). This varies with the symmetry of the polyform.
The "One-Sided" column identifies polyforms that are asymmetrical in reflection. Treating the flipped and unflipped versions of asymmetrical polyhexes as distinct polyforms (and disallowing further reflection or "flipping"), results in "one-sided" polyhexes and puzzles.
Tetrahexes
There are 7 free tetrahexes (order-4 polyhexes) and 10 one-sided tetrahexes:
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| I4 | 
|
3 | |
| J4 | 
|
12 | yes |
| O4 | 
|
3 | |
| P4 | 
|
12 | yes |
| S4 | 
|
6 | yes |
| U4 | 
|
6 | |
| Y4 | 
|
2 |
Pentahexes
There are 22 free pentahexes (order-5 polyhexes) and 33 one-sided pentahexes:
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| A5 | 
|
6 | |
| B5 | 
|
12 | yes |
| C5 | 
|
6 | |
| D5 | 
|
6 | |
| E5 | 
|
6 | |
| F5 | 
|
12 | yes |
| G5 | 
|
12 | yes |
| H5 | 
|
12 | yes |
| I5 | 
|
3 | |
| J5 | 
|
12 | yes |
| L5 | 
|
6 | |
| N5 | 
|
12 | yes |
| P5 | 
|
12 | yes |
| Q5 | 
|
12 | yes |
| R5 | 
|
12 | yes |
| S5 | 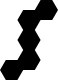
|
6 | yes |
| T5 | 
|
12 | yes |
| U5 | 
|
6 | |
| V5 | 
|
6 | |
| W5 | 
|
6 | |
| X5 | 
|
3 | |
| Y5 | 
|
6 |
Hexahexes
There are 82 free hexahexes (order-6 polyhexes) and 147 one-sided hexahexes:
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| A06 | 
|
2 | |
| A16 | 
|
12 | yes |
| A26 | 
|
12 | yes |
| C06 | 
|
6 | |
| C16 | 
|
6 | |
| C26 | 
|
12 | yes |
| C36 | 
|
12 | yes |
| C46 | 
|
12 | yes |
| C56 | 
|
12 | yes |
| C66 | 
|
12 | yes |
| C76 | 
|
12 | yes |
| E06 | 
|
6 | |
| F06 | 
|
12 | yes |
| F16 | 
|
12 | yes |
| H06 | 
|
12 | yes |
| H16 | 
|
12 | yes |
| H26 | 
|
12 | yes |
| I06 | 
|
3 | |
| J06 | 
|
12 | yes |
| J16 | 
|
12 | yes |
| J26 | 
|
12 | yes |
| J36 | 
|
12 | yes |
| J46 | 
|
12 | yes |
| K06 | 
|
12 | yes |
| L06 | 
|
12 | yes |
| L16 | 
|
12 | yes |
| L26 | 
|
12 | yes |
| L36 | 
|
12 | yes |
| M06 | 
|
12 | yes |
| M16 | 
|
12 | yes |
| M26 | 
|
12 | yes |
| M36 | 
|
6 | yes |
| M46 | 
|
6 | yes |
| N06 | 
|
6 | yes |
| N16 | 
|
12 | yes |
| O06 | 
|
1 | |
| P06 | 
|
12 | yes |
| P16 | 
|
12 | yes |
| P26 | 
|
12 | yes |
| P36 | 
|
12 | yes |
| P46 | 
|
12 | yes |
| P56 | 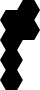
|
12 | yes |
| P66 | 
|
12 | yes |
| P76 | 
|
12 | yes |
| Q06 | 
|
12 | yes |
| Q16 | 
|
12 | yes |
| Q26 | 
|
12 | yes |
| Q36 | 
|
12 | yes |
| R06 | 
|
12 | yes |
| R16 | 
|
12 | yes |
| S06 | 
|
6 | yes |
| S16 | 
|
6 | yes |
| S26 | 
|
6 | yes |
| S36 | 
|
12 | yes |
| T06 | 
|
6 | |
| T16 | 
|
6 | |
| T26 | 
|
12 | yes |
| T36 | 
|
12 | yes |
| T46 | 
|
12 | yes |
| T56 | 
|
6 | |
| T66 | 
|
12 | yes |
| T76 | 
|
12 | yes |
| U06 | 
|
6 | |
| U16 | 
|
6 | |
| U26 | 
|
12 | yes |
| V06 | 
|
6 | |
| V16 | 
|
12 | yes |
| W06 | 
|
12 | yes |
| W16 | 
|
12 | yes |
| W26 | 
|
12 | yes |
| W36 | 
|
12 | yes |
| X06 | 
|
3 | |
| X16 | 
|
3 | |
| X26 | 
|
12 | yes |
| Y06 | 
|
6 | |
| Y16 | 
|
6 | |
| Y26 | 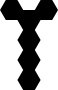
|
6 | |
| Y36 | 
|
12 | yes |
| Y46 | 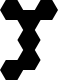
|
12 | yes |
| Y56 | 
|
12 | yes |
| Y66 | 
|
4 | yes |
| Z06 | 
|
6 | yes |
Coordinate System
Polyhex puzzles use a skewed 2-D coordinate system, where the X and Y axes are 60° apart instead of the usual 90°. The typical representation (as seen in the Polyform Puzzler solution data files) positions the Y axis vertically with the X axis 30° counter-clockwise from horizontal:
__ 3
__/ \
__/ \ / 2
__/ __/ \
__/ / __/ 1
__/ \__ \ / \
__/ __ \__/ \ / y=0
/ \ / \__/ \__/ \
3 \ / \__ __/ __/
/ \__/ \ / __/
2 \ / / \__/ 6
/ \ \__/ 5
1 \ / __/ 4
/ \__/ 3
y=0 \__/ 2
1
x=0
Each unit hexagon has 6 immediate neighbors. The neighbors of the hexagon at coordinates (x, y) are:
{(x+1, y), (x, y+1), (x-1, y-1), (x-1, y), (x, y-1), (x+1, y-1)}




