An Introduction to Polytrigs (Triangular-Grid Polysticks)
| Author: | David Goodger <goodger@python.org> |
|---|---|
| Date: | 2015-02-24 |
| Revision: | 600 |
| Web site: | http://puzzler.sourceforge.net/ |
| Copyright: | © 1998-2015 by David J. Goodger |
| License: | GPL 2 |

Contents
Polytrigs are polyforms constructed from unit line segments (edges) joined end-to-end on a regular triangular grid, also known as "triangular-grid polysticks" or "triangular polysticks".
Here is a puzzle containing all the polytrigs of order 1 through 3:
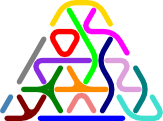
See Polytrigs: Puzzles & Solutions for many more puzzles.
The name "trig" comes from "TRIangular Grid"; a neologism I invented because "triangular-grid polysticks" is too unwieldy, especially when combined with order-prefixes (mono-, di-, tri-, tetra-, etc.; "triangular-grid tristicks"!?). I hope the name catches on.
The polytrigs can be thought of as the projective duals of polyhexes. Most of the polytrigs of order N can be derived from the polyhexes of order N+1 (i.e., joining the centers of the hexagons of a tetrahex results in a tritrig). The exceptions are the polytrigs with loops (e.g. the "O04" tetratrig), which are duals of the same order or lower-order polyhexes.
Hopefully these puzzles will begin to fill this particular gap in the polyform puzzle branch of recreational mathematics.
Prior Research
If the square polysticks don't get the respect they deserve, this is doubly true for the triangular polysticks.
—Alexandre Owen Muñiz, Puzzle Zapper Blog
Brief mention of triangular-grid polysticks is made on the Wolfram Mathworld page on Polysticks, in Alexandre Owen Muñiz's blog above, as well as in Livio Zucca's work (the original site is gone, but a mirror exists).
In January 2012 I received email from Leslie E. Shader (Ph.D., Professor Emeritus, Mathematics, University of Wyoming), who shared the results of his unpublished work on triangular-grid polysticks from around 1993.
Colin F. Brown, in addition to his work on polytwigs (hexagonal-grid polysticks), has also done some work on the quasi-polytrigs; see "Quasi-Polyforms" below.
At the Gathering for Gardner 10 (G4G10, 2012), Les Shader gave me a copy of his gift exchange paper from the Gathering for Gardner 2 or 3 (1996 or 1998), reproduced below, with permission.
If you know of any other work on this type of puzzle, please let me know!
3-Trees and a Triangle
by Leslie E. Shader, Ph.D.
[A paper from the Gathering for Gardner 2 or 3 (1996 or 1998).]
In a paper, “Polysticks”, J. Recreatinal Mathematics, vol. 22(3) 1990, Brian Barwell introduced a new type of puzzle. Instead of tiling a region in the plane or packing a region in 3-space, Barwell considered a rectangular lattice (graph paper) and used “Polysticks” to cover certain subsets of the lattice. There has also been a puzzle called “845”, I believe produced by International Puzzles and Games in Taiwan. This used 10 polysticks each with 4 unit lengths. (A polystick of length n, is a set of n unit segments joined at the ends at an angle of 90, 180, or 270 degrees.) The “845” puzzle did not allow the pieces to cross.
For “3-Trees and a Triangle” we will use 3 unit lengths joined at the ends at angles of 60, 120, 180, 240, or 300 degrees. There are exactly 12 such pieces. In the language of mathematics (graph theory), each of the pieces is either a “tree” or a “triangle”. Actually we should say Euclidean Tree since angles as well as length are important. Since we wish a physical model of this puzzle we will not allow crossings. The pieces may be rotated or turned over.
The pieces are: [sketch of the 12 tritrigs, which see]
I am including with my submission, a list of more than 300 different lattices that can be covered by subsets of the set of all pieces above. I also have included a set of solutions for each of these. But the solutions are sealed! Please try some of the puzzles before looking at the solutions. I have included a smaller set of my favorite puzzles. Those puzzles with 6 or fewer pieces are relatively easy. I classify the puzzles using 7-9 pieces as [moderately] difficult, and if the puzzle requires 10-12 pieces the puzzle is difficult. Some of the 10-12 pieces have taken me up to 20 hours to solve by hand. Of course, I didn’t now if a solution existed or not, which means an exhaustive search had to be done. Within the sealed envelope marked “solutions”, there is also a set of six puzzles that cannot be solved. I am sure there are other interesting puzzles that I have not included inthe set that I am submitting to you.
Some thoughts on the technical aspects of the puzzles. I think that the unit length should be either 7/8 in. or 1 in., the individual pieces should be injection molded with width 1/8 in and 1/2 in. deep. Care must be given to fit at the vertices where more than 1 piece come together. Several rough sketches are included. I prefer rounded corners to sharp corners. A universal base can also be injection molded and should be large enough to make most of the puzzles I have included. There should be raised traingles (corners rounded) to hold the pieces in position. The “845” puzzle used circles but I think the triangles would be better.
Finally, although the use of the trees and triangle looks entirely new, the pieces can be “fleshed out” allowing an isoceles triangle, base angle 30 degrees, to “grow” on each edge. I have included a page with two examples. Actually, we are now very close to Damert’s “Bees” puzzle except that crossings are still not allowed. Perhaps the idea of joining pieces at the vertex and not the edge (two dimensional) or at an edge and not a face (three dimensional) is an idea whose time has come. Have you seen the Rubik’s Blocks puzzle?
Polyforms
The number and names of the various orders of polytrigs are as follows:
| Order | Polyform
Name
|
Free
Polytrigs
|
One-Sided
Polytrigs
|
|---|---|---|---|
| 1 | monotrig | 1 | 1 |
| 2 | ditrigs | 3 | 3 |
| 3 | tritrigs | 12 | 19 |
| 4* | tetratrigs | 60 | 104 |
| 5* | pentatrigs | 375 | 719 |
| 6* | hexatrigs | 2613 | 5123 |
"*" above means that forms with enclosed holes exist.
The numbers of polytrigs can also be found in the following sequences from The On-Line Encyclopedia of Integer Sequences: A159867 (free) and A151539 (one-sided).
Examples of the polytrigs from order 1 (monotrig) to order 4 (tetratrigs) are given in the tables below.
The polytrigs are named with a letter-number scheme, like "I1", "C3", and "R14". The initial letter is the letter of the alphabet that the polytrig most closely resembles. In some cases, that resemblance is weak, and the letters are arbitrary. The final digit of the number represents the polyform order (how many line segments are in the polytrig). There are more tetratrigs than letters in the alphabet, so their names have an extra middle digit (numbered from 0) to differentiate the variations.
In the tables below, "Aspects" refers to the number of unique orientations that a polyform may take (different rotations, flipped or not). This varies with the symmetry of the polyform.
The "One-Sided" column identifies polyforms that are asymmetrical in reflection. Treating the flipped and unflipped versions of asymmetrical polytrigs as distinct polyforms (and disallowing further reflection or "flipping"), results in "one-sided" polytrigs and puzzles.
Tritrigs
There are 12 free tritrigs (order-3 polytrigs) and 19 one-sided tritrigs:
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| C3 | 
|
6 | |
| E3 | 
|
6 | |
| I3 | 
|
3 | |
| J3 | 
|
12 | yes |
| L3 | 
|
12 | yes |
| O3 | 
|
2 | |
| P3 | 
|
12 | yes |
| S3 | 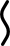
|
6 | yes |
| T3 | 
|
12 | yes |
| U3 | 
|
12 | yes |
| Y3 | 
|
2 | |
| Z3 | 
|
6 | yes |
Tetratrigs
There are 60 free tetratrigs (order-4 polytrigs) and 104 one-sided tetratrigs:
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| B04 | 
|
12 | yes |
| B14 | 
|
12 | yes |
| C04 | 
|
6 | |
| D04 | 
|
12 | yes |
| E04 | 
|
12 | yes |
| E14 | 
|
6 | |
| E24 | 
|
12 | yes |
| E34 | 
|
12 | yes |
| F04 | 
|
12 | yes |
| F14 | 
|
12 | yes |
| F24 | 
|
12 | yes |
| F34 | 
|
12 | yes |
| H04 | 
|
12 | yes |
| H14 | 
|
12 | yes |
| H24 | 
|
12 | yes |
| H34 | 
|
12 | yes |
| I04 | 
|
3 | |
| J04 | 
|
12 | yes |
| J14 | 
|
12 | yes |
| J24 | 
|
12 | yes |
| J34 | 
|
12 | yes |
| K04 | 
|
6 | |
| L04 | 
|
12 | yes |
| M04 | 
|
6 | |
| N04 | 
|
12 | yes |
| N14 | 
|
12 | yes |
| O04 | 
|
3 | |
| P04 | 
|
12 | yes |
| P14 | 
|
12 | yes |
| P24 | 
|
12 | yes |
| P34 | 
|
12 | yes |
| Q04 | 
|
12 | yes |
| Q14 | 
|
12 | yes |
| R04 | 
|
12 | yes |
| R14 | 
|
12 | yes |
| R24 | 
|
12 | yes |
| R34 | 
|
12 | yes |
| S04 | 
|
6 | yes |
| S14 | 
|
12 | yes |
| S24 | 
|
12 | yes |
| S34 | 
|
12 | yes |
| S44 | 
|
12 | yes |
| T04 | 
|
12 | yes |
| T14 | 
|
6 | |
| T24 | 
|
12 | yes |
| U04 | 
|
12 | yes |
| U14 | 
|
6 | |
| U24 | 
|
6 | |
| V04 | 
|
6 | |
| V14 | 
|
6 | |
| V24 | 
|
6 | |
| W04 | 
|
6 | |
| W14 | 
|
6 | |
| W24 | 
|
12 | yes |
| X04 | 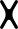
|
3 | |
| Y04 | 
|
6 | |
| Y14 | 
|
12 | yes |
| Y24 | 
|
12 | yes |
| Y34 | 
|
12 | yes |
| Z04 | 
|
6 | yes |
Quasi-Polyforms
Quasi-polyforms are polyforms where the requirement that all unit shapes be connected has been removed. In other words, quasi-polyforms are polyforms where some or all unit shapes may be separate from the others.
Without limits on the distance between unit shapes there would be an infinite number of quasi-polyforms (for orders 2 and above). We will limit the quasi-polyforms we consider to those with length-1 gaps between segments.
The number and names of the various orders of quasi-polytrigs are as follows:
| Order | Polyform
Name
|
Free
Polytrigs
|
One-Sided
Polytrigs
|
|---|---|---|---|
| 1 | monotrig [*] | 1 | 1 |
| 2 | quasi-ditrig | 9 | 13 |
| 3 | quasi-tritrigs | 140 | 259 |
| 4 | quasi-tetratrigs | 3377 | 6639 |
| [*] | With only 1 line segment, there can be no disconnected quasi-monotrig. The set of the regular (fully-connected) monotrigs is identical to the set of quasi-monotrigs, and consists of one piece: the "I1" monotrig. |
Examples of the quasi-polytrigs of order 2 (quasi-ditrigs) are given in the table below. See the table legend above for column descriptions.
Quasi-Ditrigs
There are 9 free quasi-ditrigs (order-2 quasi-polytrigs) and 13 one-sided quasi-ditrigs:
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| C12 | 
|
6 | |
| I02 | 
|
3 | |
| I12 | 
|
3 | |
| L02 | 
|
6 | |
| L12 | 
|
12 | yes |
| P12 | 
|
12 | yes |
| S12 | 
|
6 | yes |
| V02 | 
|
6 | |
| Z12 | 
|
6 | yes |
Coordinate System
Polytrig puzzles use a pseudo-3D skewed coordinate system, where the X and Y axes are 60° apart instead of the usual 90°. The typical representation (as seen in the Polyform Puzzler solution data files) positions the X axis horizontally with the Y axis 30° clockwise from vertical.
The (X,Y) 2-dimensional coordinate identifies the lower-left corner of the (X,Y,0) triangle in a polyiamond grid. The first three line segments emanating from this point share the (X,Y) coordinate, and the Z dimension is used for the direction of the line segment:
Intersections
As there is the possibility for polytrigs to cross each other at any (X,Y) intersection, the solution algorithm needs to prevent such crossings. Unlike with polysticks, the intersections are not simple (either used or available); multiple polyforms can use an intersection simultaneously.
In the puzzle matrix, we represent contstraints on intersections via up to 6 additional columns per intersection [†], in the form i(X,Y,Z) (or "X,Y,Zi"). This means that the segment in direction Z cannot go through the intersection, (X,Y). These are the Z directions:
2 1
\ /
3___\/___0
/\
/ \
4 5
| [†] | Possibly fewer columns for intersections at the edge of a puzzle shape. This represents a possible future optimization. Note that since there are already 3 line segments originating at each intersection, the cost of intersection constraints is 2 per segment, which effectively multiplies the number of coordinate columns by 3. Polytrig puzzle matrixes |
These intersection constraints are secondary columns, meaning that at most one polyform may use or fill a column. Unlike primary columns, secondary columns may remain unused/unfilled.
For each polyform, we check the angle between each pair of line segments. Both ends of each segment must be checked, but only in one direction (counter-clockwise) to avoid duplication. For any two line segments, there are six possibilities:
B / A
____/___ D ____ E ____ F ____
/ \
C / D' \
- A: 60° (adjacent) -- no constraints are added.
- B: 120° (one-gapper) -- 3 constraints are added: the 2 line segments themselves (e.g. Z={1,3}), plus the gap in-between (e.g. Z=2).
- C: 180° (two-gapper) -- 4 constraints are added: the 2 line segments (e.g. Z={3,0}), plus the two gaps (e.g. Z={4,5}). Note that the gaps on the opposite side will be added when the other line segment is checked.
- D: 240° (three-gapper) -- no constraints are added. However, D' is a case of a 120° one-gapper (case B).
- E: 300° (four-gapper) -- no constraints are added.
- F: 360° (five-gapper or stub; only one segment involved) -- no constraints are added.
Only cases B & C require constraints.
If an intersection constraint is already used (or otherwise unavailable), no other polyform with the same contstraint may be placed in the puzzle solution.



