Polytrigs (Triangular-Grid Polysticks): Puzzles & Solutions
| Author: | David Goodger <goodger@python.org> |
|---|---|
| Date: | 2015-02-24 |
| Revision: | 600 |
| Web site: | http://puzzler.sourceforge.net/ |
| Copyright: | © 1998-2015 by David J. Goodger |
| License: | GPL 2 |

Contents
Tritrigs
These puzzles use the 12 tritrigs, for a total of 36 line segments on the triangular grid.
3x1 semi-regular hexagon ring: 1 solution

5x2 paralellogram: 9 solutions

5x3 trapezoid ring: 1 solution

6x2 trapezoid: 8 solutions

Stacked 2x2x1 elongated hexagons: 9 solutions

5x3 jagged trapezoid: 1 solution

Spiked triangle: 6 solutions

Length-5 triangles with 9 segments omitted:
Hearts (design by Leslie E. Shader):
Length-2 hexagons with 6 segments omitted:
One-Sided Tritrigs
7 of the 12 tritrigs are asymmetrical, therefore there are 19 one-sided tritrigs. The puzzles take up 57 segments on the triangular grid.
4x1 semi-regular hexagon: solutions incomplete

Length-6 triangle: solutions incomplete

5x2 butterfly: solutions incomplete

3x3 chevron: solutions incomplete

2x4 chevron 1: solutions incomplete

2x4 chevron 2: solutions incomplete

8x1 chevron: solutions incomplete

7x3 trapezoid 1: solutions incomplete

7x3 trapezoid 2: solutions incomplete

9x2 trapezoid 1: solutions incomplete

9x2 trapezoid 2: solutions incomplete

Tri-lobed cuboid: 9 solutions

Polytrigs of Order 2 & 3
These puzzles use the 3 ditrigs and 12 tritrigs, for a total of 42 line segments on the triangular grid.
Hexagon: 1,118 solutions

Triangle ring: 821 solutions

Three congruent groups:
First, divide the twelve tritrigs into three groups of four, and add one of the ditrigs to each group. Find a 14-line region that each (equally divided) group will tile.
Finally, find a solution to the three congruent groups problem such that the three groups can be combined into a symmetrical shape. The more symmetries the better.
Example 1: 4 solutions.

The groups above combine nicely in several ways (the numbers of solutions given is when restricted to combinations of the congruent groups above):
Trefoils: these are the unrestricted versions of three of the combined shapes of the three congruent groups puzzle, above.
Polytrigs of Order 1 Through 3
These puzzles use the 1 monotrig, 3 ditrigs, and 12 tritrigs, for a total of 43 line segments on the triangular grid.
4x3 parallelogram: solutions incomplete

5x4 trapezoid: solutions incomplete
3x2 chevron: solutions incomplete

4x2 butterfly: solutions incomplete
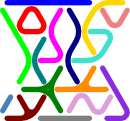
7x2 trapezoid 1: solutions incomplete

7x2 trapezoid 2: solutions incomplete

Length-5 triangle, with various holes:
One-Sided Polytrigs of Order 1 Through 3
These puzzles use the 1 monotrig, 3 ditrigs, and 19 one-sided tritrigs, for a total of 64 line segments on the triangular grid.
9x2 parallelogram: solutions incomplete

5x4 parallelogram: solutions incomplete

10x2 trapezoid: solutions incomplete

7x4 trapezoid: solutions incomplete

6x2 butterfly: solutions incomplete

4x2 elongated hexagons, with various holes:
8x3 trapezoids, with various holes:
9x1 chevron: solutions incomplete

X (designed for G4G10): solutions incomplete
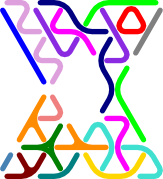
Quasi-Ditrigs
These puzzles use the 9 quasi-ditrigs, for a total of 18 line segments on the triangular grid. See Quasi-Polyforms in An Introduction to Polytrigs.
Triangle (design by Colin F. Brown): 266 solutions

Triangle stack: 63 solutions

Jagged triangle: 87 solutions

Two triangles:

8 solutions (design by Colin F. Brown, as "diabolo")
Starburst (design by Colin F. Brown): 298 solutions

Satellite (design by Colin F. Brown): 24 solutions

Quasi-Polytrigs of Order 1 and 2
These puzzles use the monotrig and the 9 quasi-ditrigs, for a total of 19 line segments on the triangular grid. See Quasi-Polyforms in An Introduction to Polytrigs.
Elongated Hexagon 2x1: 542 solutions

Trapezoid 5x1: 358 solutions