An Introduction to Polytwigs (Hexagonal-Grid Polysticks)
| Author: | David Goodger <goodger@python.org> |
|---|---|
| Date: | 2015-02-24 |
| Revision: | 600 |
| Web site: | http://puzzler.sourceforge.net/ |
| Copyright: | © 1998-2015 by David J. Goodger |
| License: | GPL 2 |

Contents
Polytwigs (a.k.a. polycules) are polyforms constructed from unit line segments (edges) joined end-to-end on a regular hexagonal grid. Unit line segments on a square grid are called "polysticks", so polytwigs could also be called "polysticks on a hexagonal grid" or "hexagonal-grid polysticks" or "hexagonal polysticks". The polytwigs are a subset of the polytrigs (triangular-grid polysticks); polytwigs would fit on a polytrig grid, but there are a lot fewer of them.
Here is a puzzle containing all the polytwigs of order 1 through 5:

And here is a puzzle containing all the hexatwigs (order 6):

See Polytwigs: Puzzles & Solutions for many more puzzles.
Most of the polytwigs of order N can be thought of as the projective duals of the polyiamonds of order N+1 (i.e., joining the centers of the triangles of a hexiamond results in a pentatwig). The exceptions are the polytwigs with loops (e.g. the "O06" hexatwig), which are duals of the same order or lower-order polyiamonds.
I invented the name "polytwigs" because "hexagonal-grid polysticks" is too unwieldy, especially when combined with order-prefixes (mono-, di-, tri-, tetra-, etc.; "hexagonal-grid tristicks"!?). The name comes from "twig" being a small stick, often bent and branching. "Polytwig" is also similar to "polytrig", the name I invented for triangular-grid polytsicks. I hope these names catch on.
Prior Research
When I began working on the hexagonal-grid polysticks, I was unable to find any references to prior research. While (to my knowledge) nothing seems to have been published, I couldn't believe that this was a completely novel idea — an intuition that proved to be true.
In February 2012 I received email from Mr. Colin F. Brown, a puzzle enthusiast from Dudley, England, who shared the results of his unpublished work on hexagonal-grid polysticks from the late 1970s and early 1980s. Mr. Brown wrote,
I did name them ‘Polycules’, from the fact that sea sponges have spicules that resemble a tri-cule (your 3-stick hexagon gridded ‘polytwig’) each segment being set at 120° apart. I also gave each pentacule a name...
See the Wikipedia article on "sponge spicules" for an image demonstrating the resemblance. In fact, Mr. Brown used the term "polycules" for sqare-grid polysticks and triangular-grid polytrigs as well (prefixed with "rectangular-", "triangular-", and "hexagonal-"), but:
... for constructional problems, I chose the hexagonal stick forms, partly because the rectangular and triangular types admitted tilings and constructions with ‘crossings’ – impossible with polytwigs.
I'll use "polycules" as a synonym for "polytwigs" here. Mr. Brown's pentacule names are listed in the pentatwigs section below. See Polytwigs: Puzzles & Solutions for examples of several of Mr. Brown's puzzle constructions.
Mr. Brown also explored the quasi-tritwigs with gaps between segments limited to length-1; see Quasi-Polyforms below.
At the Gathering for Gardner 10 (G4G10, 2012), Les Shader gave me a copy of a page from a Russian journal "Charade" ("ШАРАДА"), N6(6), December 1993. It featured a solution to the "Hexonet" puzzle ("ГЕКСОСЕТИ"), exactly the pentatwigs triangle (side length 5). Thanks to Tanya Khovanova of MIT for translating.
If you know of any other work on this type of puzzle, please let me know!
Polyforms
The number and names of the various orders of polytwigs are as follows:
| Order | Polyform
Name
|
Free
Polytwigs
|
One-Sided
Polytwigs
|
|---|---|---|---|
| 1 | monotwig | 1 | 1 |
| 2 | ditwig | 1 | 1 |
| 3 | tritwigs | 3 | 4 |
| 4 | tetratwigs | 4 | 6 |
| 5 | pentatwigs | 12 | 19 |
| 6 | hexatwigs | 27 | 49 |
| 7 | heptatwigs | 78 | 143 |
The numbers of polytwigs can also be found in the following sequences from The On-Line Encyclopedia of Integer Sequences: A197459 (free) and A197460 (one-sided).
Examples of the polytwigs from order 1 (monotwig) to order 6 (hexatwigs) are given in the tables below.
The polytwigs are named with a letter-number scheme, like "I1", "C3", and "R16". The letter part is the letter of the alphabet that the polytwig most closely resembles. In some cases, that resemblance is weak, and the letters are arbitrary. The final digit of the number represents the polyform order (how many line segments are in the polytwig). There are more hexatwigs than letters in the alphabet, so their names have an extra middle digit (numbered from 0) to differentiate the variations.
In the tables below, "Aspects" refers to the number of unique orientations that a polyform may take (different rotations, flipped or not). This varies with the symmetry of the polyform.
The "One-Sided" column identifies polyforms that are asymmetrical in reflection. Treating the flipped and unflipped versions of asymmetrical polytwigs as distinct polyforms (and disallowing further reflection or "flipping"), results in "one-sided" polytwigs and puzzles.
Tritwigs
There are 3 free tritwigs (order-3 polytwigs) and 4 one-sided tritwigs:
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| C3 | 
|
6 | |
| S3 | 
|
6 | yes |
| Y3 | 
|
2 |
Tetratwigs
There are 4 free tetratwigs (order-4 polytwigs) and 6 one-sided tetratwigs:
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| C4 | 
|
6 | |
| P4 | 
|
12 | yes |
| W4 | 
|
6 | |
| Y4 | 
|
12 | yes |
Pentatwigs
There are 12 free pentatwigs (order-5 polytwigs, a.k.a. pentacules) and 19 one-sided pentatwigs. Colin F. Brown's original pieces and their evocative names are listed in the "Pentacule" and last "Name" columns.
| Name | Image | Aspects | One-Sided | Pentacule | Name |
|---|---|---|---|---|---|
| C5 | 
|
6 | 
|
Bowl | |
| H5 | 
|
12 | yes | 
|
Chair |
| I5 | 
|
6 | yes | 
|
Stick |
| L5 | 
|
12 | yes | 
|
Signpost |
| P5 | 
|
12 | yes | 
|
Hook |
| R5 | 
|
12 | yes | 
|
Pipe |
| S5 | 
|
6 | yes | 
|
Snake |
| T5 | 
|
6 | 
|
Bird | |
| U5 | 
|
6 | 
|
Bridge | |
| W5 | 
|
12 | yes | 
|
Club |
| X5 | 
|
6 | 
|
Trestle | |
| Y5 | 
|
6 | 
|
Fork |
Hexatwigs
There are 27 free hexatwigs (order-6 polytwigs) and 49 one-sided hexatwigs:
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| C06 | 
|
12 | yes |
| F06 | 
|
12 | yes |
| H06 | 
|
12 | yes |
| H16 | 
|
12 | yes |
| I06 | 
|
6 | |
| J06 | 
|
12 | yes |
| L06 | 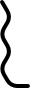
|
12 | yes |
| L16 | 
|
12 | yes |
| L26 | 
|
12 | yes |
| M06 | 
|
6 | |
| O06 | 
|
1 | |
| Q06 | 
|
12 | yes |
| Q16 | 
|
12 | yes |
| Q26 | 
|
12 | yes |
| R06 | 
|
12 | yes |
| R16 | 
|
12 | yes |
| S06 | 
|
12 | yes |
| S16 | 
|
12 | yes |
| S26 | 
|
12 | yes |
| U06 | 
|
6 | |
| V06 | 
|
6 | |
| W06 | 
|
12 | yes |
| X06 | 
|
12 | yes |
| X16 | 
|
12 | yes |
| Y06 | 
|
4 | yes |
| Y16 | 
|
12 | yes |
| Y26 | 
|
12 | yes |
Quasi-Polyforms
Quasi-polyforms are polyforms where the requirement that all unit shapes be connected has been removed. In other words, quasi-polyforms are polyforms where some or all unit shapes may be separate from the others.
Without limits on the distance between unit shapes there would be an infinite number of quasi-polyforms (for orders 2 and above). We will limit the quasi-polyforms we consider to those with length-1 gaps between segments.
The number and names of the various orders of quasi-polytwigs are as follows:
| Order | Polyform
Name
|
Free
Polytwigs
|
One-Sided
Polytwigs
|
|---|---|---|---|
| 1 | monotwig [*] | 1 | 1 |
| 2 | quasi-ditwig | 3 | 4 |
| 3 | quasi-tritwigs | 17 | 28 |
| 4 | quasi-tetratwigs | 114 | 214 |
| 5 | quasi-pentatwigs | 966 | 1885 |
| [*] | With only 1 line segment, there can be no disconnected quasi-monotwig. The set of the regular (fully-connected) monotwigs is identical to the set of quasi-monotwigs, and consists of one piece: the "I1" monotwig. |
Examples of the quasi-polytwigs of order 2 (quasi-ditwigs) and order 3 (quasi-tritwigs) are given in the tables below. See the table legend above for column descriptions.
Quasi-Ditwigs
There are 3 free quasi-ditwigs (order-2 quasi-polytwigs) and 4 one-sided quasi-ditwigs:
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| C2 | 
|
6 | |
| L2 | 
|
6 | |
| S2 | 
|
6 | yes |
Quasi-Tritwigs
In his prior research, Colin F. Brown showed that in addition to the 3 free connected tritwigs, there are 5 semi-connected (one gap) quasi-tritwigs and 9 disconnected (two gaps) quasi-tritrigs, for a total of 17 free quasi-tritwigs (order-3 quasi-polytwigs). There are 28 one-sided quasi-tritwigs.
| Name | Image | Aspects | One-Sided |
|---|---|---|---|
| C03 | 
|
6 | |
| C13 | 
|
12 | yes |
| C23 | 
|
2 | |
| H13 | 
|
12 | yes |
| I13 | 
|
6 | yes |
| P13 | 
|
12 | yes |
| P23 | 
|
12 | yes |
| P33 | 
|
12 | yes |
| S03 | 
|
6 | yes |
| S13 | 
|
6 | yes |
| T13 | 
|
6 | |
| U13 | 
|
6 | |
| W13 | 
|
12 | yes |
| W23 | 
|
12 | yes |
| Y03 | 
|
2 | |
| Y13 | 
|
12 | yes |
| Y23 | 
|
6 |
Coordinate System
Polytwig puzzles use a pseudo-3D skewed coordinate system, where the X and Y axes are 60° apart instead of the usual 90°. The typical representation (as seen in the Polyform Puzzler solution data files) positions the Y axis vertically with the X axis 30° counter-clockwise from horizontal. Solution graphics are often rotated so the X axis is horizontal, and the Y axis 30° clockwise from vertical.
The (X,Y) 2-dimensional coordinate identifies the lower-left corner of the (X,Y) hexagon in a polyhex grid (a honeycomb with hexagons with horizontal tops & bottoms). The three line segments emanating from this point share the (X,Y) coordinate, and the Z dimension is used for the direction of the line segment:
Since only three line segments may emanate from each (X,Y) intersection, there is no possibility for polytwigs to cross each other and no need to keep track of intersections. This separates polytwigs from polysticks and polytrigs, where such considerations are crucial.

